What Is Systematic Sampling? | Definition & Examples
Systematic sampling, also known as systematic random sampling, is a probability sampling technique that involves selecting every nth element from the population, where n is the predetermined sampling interval.
The sampling method provides you with a representative sample of a population as long as the order of the population is random or near-random (e.g., alphabetically ordered). The data collected from this sample can be used to draw conclusions about your entire research population.
To conduct the survey, the university decides to use systematic sampling. They start by creating a list of all the students in the course, numbered from 1 to 500.
To select the sample, they decide to use a sampling interval of 10. This means they will select every 10th student from the list until they’ve reached their desired sample size.
What is systematic sampling?
Systematic sampling is a technique used to select a sample of elements from a population. It involves selecting every nth element from the population, where n is the sampling interval. This means that the sample is selected in a regular and systematic way, rather than completely at random.
In systematic sampling, the first element to be selected is usually chosen at random, and then the remaining elements are selected by moving forward n steps in the list. For example, if you want to select every 5th element from a list of 100 elements, you would start by selecting the first element (randomly), and then select every 5th element thereafter.
This method is often used in place of simple random sampling when a complete list of the population can’t be obtained.
Since the order in which supporters exit is usually random, you should still obtain a representative sample of supporters.
When not to use systematic sampling
Systematic sampling is appropriate for populations that have no order at all or an ascending or descending order. In all cases, the sample will include subjects from the top and bottom of the list.
You should avoid using systematic sampling when your population has a cyclical or periodic order. This could result in only including individuals with a specific trait (e.g., a specific age group) in your sample.
Systematic sampling example
- The researcher first creates an alphabetically ordered list of all 5,000 employees in the corporation.
- Then, they determine the sampling interval by dividing the total number of employees (5,000) by the desired sample size (200). This results in a sampling interval of 25, which means every 25th employee will be selected for the sample.
- The researcher selects a random starting point from the list, for example 123.
- They then select every 25th employee from the list, starting from the random starting point (123, 148, 173, etc.). They continue until they reach a total of 200 employees.
Stratified vs systematic sampling
Stratified sampling and systematic sampling are often confused because they’re both types of probability sampling. They do, however, differ in their approach to selecting a sample from a population.
- Stratified sampling is a technique where the population gets divided into smaller groups or strata (based on one or more characteristics) before randomly selecting subjects from each stratum.
- Systematic sampling is a technique where researchers select subjects from a list or database at a regular interval (e.g., every 10th subject).
During the initial stages of the research process, the researcher is considering two sampling methods to draw a sample.
Stratified sampling
The researcher could divide the population into three strata based on gender:
- Stratum 1: Female (60% of the population)
- Stratum 2: Male (30% of the population)
- Stratum 3: Nonbinary (10% of the population)
They could then use simple random sampling to draw a proportional sample from each stratum. The final sample would have the same gender distribution as the total population.
Systematic sampling
The researcher could create a list of all consumers and determine the sampling interval (n) by dividing the total number of consumers (10,000) by the desired sample size (500), which gives a sampling interval of 20.
The researcher uses a random number generator to select a random starting point from the list and then selects every 20th consumer.
The resulting sample consists of 500 consumers.
Since this method doesn’t ensure that the sample will be representative of each gender identity, the researcher decides to go with stratified sampling.
Systematic sampling advantages
Systematic sampling comes with many advantages.
-
Efficient
Systematic sampling is a quick and efficient way to select a sample from a large population. It requires minimal effort to select the sample, as it involves selecting every nth unit from the list. This makes it easy to implement and cost-effective.
-
Representative
Systematic sampling is a type of random sampling (or probability sampling), which means that it can produce a representative sample of the population. The sample is likely to be representative of the population because it is based on a random starting point and a fixed sampling interval.
-
Reduced bias
Systematic sampling can help reduce bias in the sample selection process, as it is based on a random starting point and a fixed sampling interval. This usually results in a more representative sample than samples selected through non-probability sampling.
Systematic sampling disadvantages
Systematic sampling also has its disadvantages.
-
Limited representation
Systematic sampling may not guarantee representation of specific subgroups within the population, such as certain demographics, industries, or geographic regions. For example, if the population is concentrated in certain areas, systematic sampling may not capture the variation in those areas.
-
Not suitable for skewed distributions
Systematic sampling may not be effective when dealing with populations with highly skewed distributions or outliers. The sample may not capture these extreme values, leading to biased estimates of population characteristics.
-
Vulnerable to sampling bias
Systematic sampling can be vulnerable to sampling bias, particularly if the starting point is not truly random. The choice of the sampling interval (e.g., every 5th unit) can also introduce bias. If the interval is too small, the sample may not be representative of the population. If the interval is too large, the sample may not capture all the variation in the population.
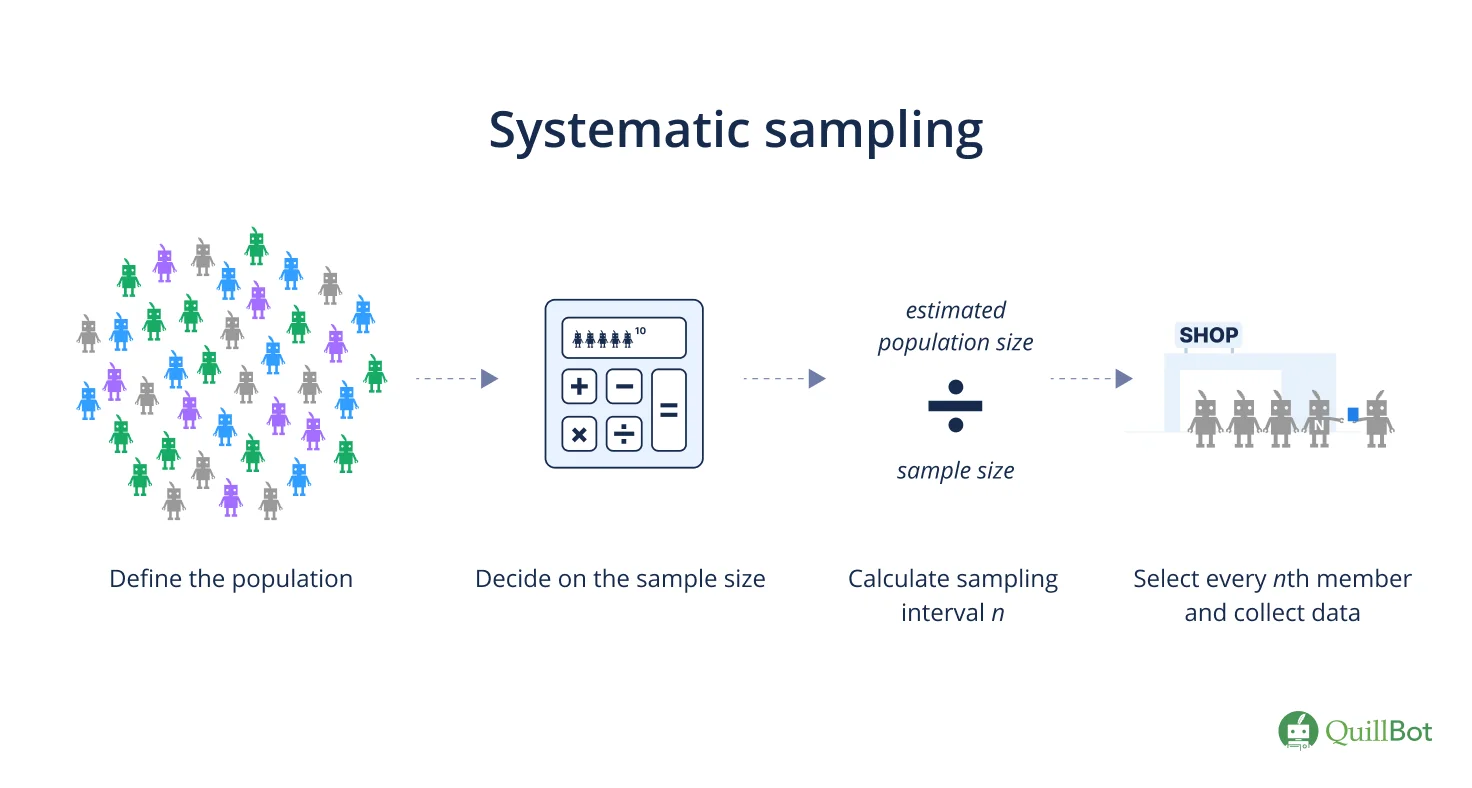
Systematic sampling steps
Systematic sampling consists of four steps:
Step 1: Define the population
First, you decide on your population. You can do this ahead of time or while collecting data.
- Ahead of time. In this case, you obtain a complete list of the population before you start collecting data. You select subjects from the list at a regular interval.
- During data collection. In this case, you are unable to obtain a list of the population in advance. Instead, you systematically approach subjects at the moment of data collection. You should take into account timing and location for sampling to ensure you cover the full population.
The first method is preferable as it lowers the risk of introducing bias.
The researcher obtains a list of all patients with type 2 diabetes who receive treatment at the clinic (2,500 people).
Step 2: Decide on the sample size
It’s important to choose an appropriate sample size to minimize the risk of sampling bias. In most cases, you can use an online sample size calculator.
You enter your chosen confidence level and margin of error (confidence interval), as well as the (estimated) population size and standard deviation of all variables you’re interested in measuring. The calculator will provide you with the best sample size for your research.
Step 3: Calculate sampling interval n
You calculate your sampling interval n by dividing the population size by your sample size. It doesn’t have to be an exact calculation.
Step 4: Select the sample
You possess a full list of the population, so you can randomly select a starting point and select every nth member to be included in your sample.
If you didn’t have a list, you’d choose every nth member of the sample while collecting data. For instance, you’d collect data from every nth customer that leaves a store.
As in cluster sampling or simple random sampling, it’s important that the subjects you’ve selected actually take part in your research. You might introduce research bias if the subjects that don’t participate decline for reasons connected to your variables of interest. This, in turn, can affect the validity of your results.
Then, they can start data collection using a technique that suits their research design (e.g., experimental design or descriptive research).
Frequently asked questions about systematic sampling
- Is systematic sampling biased?
-
Systematic sampling is a probability sampling method, which typically ensures a lower risk of bias than nonprobability sampling methods.
However, systematic sampling can be vulnerable to sampling bias, especially if the starting point isn’t truly random. The choice of sampling interval can also introduce bias:
- If the interval is too small, the sample can lack representativeness of the population.
- If the interval is too large, the sample might not capture all the variation that exists in the population.
- Is systematic sampling random?
-
Systematic sampling is a random sampling method. Another name for random sampling is probability sampling.
In systematic sampling, the researcher chooses a random starting point in a list of the population (e.g., by using a random number generator) before selecting subjects for the sample at a regular sampling interval (n). The random starting point and regular interval ensure the random nature of this sampling method.
- What is the formula for systematic sampling?
-
You can use a formula to calculate the sampling interval in systematic sampling, which is a probability sampling method where the researcher systematically selects subjects for their sample at a regular interval.
You can calculate the sampling interval (n) by dividing the total population by the desired sample size.
- Formula: n = population size/sample size
- Example: I = 2,000/200 = 10
In some cases, people might use a different letter to indicate the sampling interval (e.g., k). This is irrelevant to the use of the formula.
- What’s the difference between stratified and systematic sampling?
-
Stratified sampling and systematic sampling are both probabilistic sampling methods used to obtain representative samples from a population, but they differ significantly in their approach and execution.
- Stratified sampling involves dividing the population into distinct subgroups (strata) based on specific characteristics (e.g., age, gender, income level) and then randomly sampling from each stratum. It ensures representation of all subgroups within the population.
- Systematic sampling involves selecting elements from an ordered population at regular intervals, starting from a randomly chosen point. For example, you have a list of students from a school and you choose students at an interval of 5. This is a useful method when the population is homogeneous or when there is no clear stratification. It’s much easier to design and less complex than stratified sampling.
- When is it inappropriate to use systematic random sampling?
-
It is inappropriate to use systematic random sampling when your population has a periodic or cyclic order. This could result in only including individuals with a specific characteristic (e.g., age) in your sample.
Systematic sampling example: Unrepresentative sample Your list of employees alternates between men, women, and nonbinary people. You select every third individual, which means you’re only selecting nonbinary people. This wouldn’t be a representative sample because the sample doesn’t contain any people who identify as men or women, whereas they make up most of the population.
Cite this Quillbot article
We encourage the use of reliable sources in all types of writing. You can copy and paste the citation or click the "Cite this article" button to automatically add it to our free Citation Generator.
Merkus, J. (2025, November 26). What Is Systematic Sampling? | Definition & Examples. Quillbot. Retrieved December 2, 2025, from https://quillbot.com/blog/research/systematic-sampling/