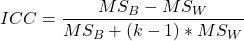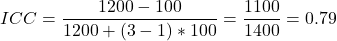Get creative with full-sentence rewrites
Paraphraser
Proofread your papers with one click
Grammar Checker
Avoid unintentional plagiarism
Plagiarism Checker
  1. Home
  2. Research
  3. What Is Inter-Rater Reliability? | Definition & Examples

What Is Inter-Rater Reliability? | Definition & Examples

Published on October 24, 2025 by Julia Merkus, MA

Inter-rater reliability is the degree of agreement or consistency between two or more raters evaluating the same phenomenon, behavior, or data.

In research, it plays a crucial role in ensuring that findings are objective, reproducible, and not dependent on a single observer’s judgment. Whether you’re analyzing questionnaire responses, coding interview transcripts, or assessing behavioral outcomes, strong inter-rater reliability boosts the credibility of your results.

The method to calculate inter-rater reliability depends on the type of data (e.g., nominal, ordinal, interval, or ratio) and the number of raters. The most common methods include Cohen’s kappa (for two raters), Fleiss’ kappa (for three or more raters), and the Intraclass Correlation Coefficient (for continuous data).

Example: Inter-rater reliability in qualitative research
A team of psychologists conducts qualitative research to examine workplace stress. They code open-ended interview responses to identify themes such as “workload pressure,” “lack of support,” and “burnout symptoms.”

During the thematic analysis, each researcher independently reads the transcripts and assigns codes to relevant passages. If the coders consistently label the same responses with the same themes, the study demonstrates high inter-rater reliability. This consistency ensures that the findings reflect real patterns in the participants’ experiences, rather than subjective interpretations or biases from individual researchers. This helps reduce observer bias.

Tip
If you need to write a research report, thesis, or journal article, ensuring your grammar and clarity are top-notch is just as important as strong research methods. Use our Grammar Checker to catch errors and make your writing professional and polished.

Free Grammar Checker

Inter-rater reliability examples

Inter-rater reliability is a critical concept across many fields because it ensures that measurements and observations are consistent and trustworthy, regardless of who is conducting the assessment.

By using reliable coding, scoring, or evaluation methods, researchers can reduce subjective bias and strengthen the validity of their findings.

Inter-rater reliability in psychology example

Example: Inter-rater reliability in psychology
A team of psychologists conducted a quasi-experimental design to investigate children’s responses to stress in a lab setting. Children participated in structured tasks designed to elicit stress, such as solving challenging puzzles under time constraints.Two observers independently recorded specific behaviors (e.g., fidgeting, facial expressions, verbal complaints) using predefined categories such as “none,” “mild,” or “severe.”

By calculating inter-rater reliability, the researchers ensured that the behavioral ratings were consistent across observers and not influenced by individual bias. High inter-rater reliability supports the internal validity of the study, confirming that observed differences truly reflect the experimental conditions rather than the subjective judgments.

Inter-rater reliability in healthcare example

Example: Inter-rater reliability in healthcare 
A research team at a hospital conducts a cross-sectional study to evaluate patients’ mobility after orthopedic surgery. Nurses use a standardized Likert scale questionnaire to rate patients’ ability to perform specific movements, such as sitting, standing, and walking.

Multiple nurses independently score each patient, and the inter-rater reliability is calculated to ensure that the ratings are consistent across observers. The consistency is crucial for monitoring recovery trends, guiding treatment decisions, and comparing outcomes across different hospitals. It also supports the study’s external validity, making it easier to generalize findings to the broader population of postoperative patients.

Inter- vs intra-rater reliability

When discussing reliability, it’s important to distinguish between inter-rater and intra-rater reliability, as both play crucial roles in ensuring accurate and consistent measurements in research.

  • Inter-rater reliability measures the consistency of ratings across different observers assessing the same phenomenon. It ensures that findings are objective and reproducible, regardless of who collects the data.
  • Intra-rater reliability measures the consistency of a single observer when assessing the same phenomenon multiple times. It ensures that an individual rater’s measurements are stable and not influenced by fatigue, memory, or subjective shifts.
Inter- vs. intra-rater reliability example
A research team conducts a study assessing pain levels in postoperative patients using observational ratings. Nurses evaluate patients’ facial expressions, body movements, and verbal cues to assign a pain score from 0 to 10.

Inter-rater reliability

Three different nurses independently assess the same group of 20 patients at the same time. The researchers calculate the ICC to determine how consistently the different nurses rate each patient. High inter-rater reliability indicates that the pain scores are not dependent on which nurse is observing.

Intra-rater reliability

One of the nurses re-evaluates the same patients’ pain levels two days later without referencing the previous scores. The researcher calculates ICC to see if this nurse’s ratings are consistent over time. High intra-rater reliability indicates that the nurse’s scoring is stable.

How to calculate inter-rater reliability

The method to calculate inter-rater reliability depends on the type of data and the number of raters. The goal is to determine how consistently different observers assess the same phenomenon. Using the right formula ensures your measurements are reliable, reproducible, and credible.

The four most common methods are:

  • Cohen’s kappa (two raters, categorical data)
  • Fleiss’ kappa (three or more raters, categorical data)
  • Intraclass Correlation Coefficient (continuous data)
  • Percent agreement (simple, but limited, method)

Cohen’s kappa

Cohen’s kappa (κ) is used when two raters classify items into categories (nominal data or ordinal data). It accounts for the agreement expected by chance, providing a more accurate measure than simple percent agreement.

The formula for Cohen’s Kappa is:

\kappa = \dfrac {{{P}_o} - {{P}_e}}{{1} - {P_e}}

Where:

  • Po = observed proportion of agreement between raters
  • Pe = expected agreement by chance
Example: Calculating inter-rater reliability with Cohen’s kappa
Imagine descriptive research in psychology aiming to document common signs of test anxiety in students during exam simulations. Two researchers independently observe 50 students and classify each student as either “anxious” or “not anxious” based on behaviors like nail-biting, fidgeting, or avoidance of eye contact.

The results look like this:

Rater 2: Anxious Rater 2: Not anxious Total
Rater 1: Anxious 20 5 25
Rater 1: Not anxious 10 15 25
Total 30 20 50
    1. Calculate observed agreement (Po)

{P}_o = \dfrac {{{20 + 15}}}{50}} = {0.70}

    1. Calculate expected agreement (Pe)

{P}_e = \dfrac {{{25*30}}}{50^2}} + \dfrac {{{25*20}}}{50^2}} = {0.30 + 0.20} = {0.50}

    1. Apply Cohen’s kappa formula

\kappa = \dfrac {{{P}_o} - {{P}_e}}{{1} - {P_e}} = \dfrac {{{0.70 - 0.50}}}{1 - 0.50}} = {0.40}

A kappa of 0.40 indicates only moderate agreement between the two observers. To ensure more robust results, they could set up training sessions or better guidelines before conducting another study.

Fleiss’ kappa

When three or more raters are involved for categorical data, Fleiss’ kappa extends Cohen’s approach to handle multiple observers.

Example: Calculating inter-rater reliability with Fleiss’ kappa
Researchers use a case study to examine how consistently medical students identify early signs of melanoma in clinical images. The team wants to ensure that students’ visual assessments are reliable before integrating this diagnostic exercise into a larger experimental design on diagnostic accuracy.

To test this, five raters (medical students) each review 20 skin lesion photographs and classify them as either:

  • Likely benign
  • Possibly malignant
  • Clearly malignant

Since there are more than two raters, the researchers use Fleiss’ kappa to measure agreement across the multiple observers.

A simplified version of the data might look like this (the data for 5 out of the 20 images is shown here):

Image Likely benign Possibly malignant Clearly malignant Total raters
1 3 2 0 5
2 0 4 1 5
3 1 1 3 5
4 5 0 0 5
5 2 2 1 5

Step 1: Calculate agreement for each item

For each image, Fleiss’ kappa looks at how many pairs of raters agreed on the same category. The formula for the proportion of agreement for each image is:
P_i = \dfrac {{{1}}}{n(n-1)} \sum_{j}{{n_{ij}({n}_{ij}-1)}

Where:

  • n = number of raters
  • nij = number of raters who chose category j for image i

For example, for image 1:
P_1 = \dfrac {{{1}}}{5(5-1)}*[(3*2) + (2*1) + (0*-1)] = \dfrac {{{8}}}{20} = {0.40}
Each image gets its own Pi and then you average them to get P, the mean observed agreement across all items.

Step 2: Calculate the expected agreement

Next, compute how often each category is chosen overall (across all raters and items). For example, across all 20 images:

  • Likely benign: 40% of all ratings
  • Possibly malignant: 35% of all ratings
  • Clearly malignant: 25% of all ratings

Then calculate:
P_1 = {{{(0.40^2)+(0.35^2)+(0.25^2) = 0.16 + 0.12 + 0.06 = 0.34}}}
Step 3: Apply Fleiss’ kappa formula

The standard formula to calculate Fleiss’ kappa is:
P_e = \dfrac {{{\bar{P}-P_e}}}{1-P_e}}
If the average observed agreement (P) across all items is 0.60:
\kappa = \dfrac {{{0.60-0.34}}}{1-0.34}} = \dfrac {{{0.26}}}{0.66} \approx 0.39
A κ of 0.39 indicates fair agreement among the five medical students.

Intraclass Correlation Coefficient (ICC)

The Intraclass Correlation Coefficient (ICC) is used when the intra-rater reliability is calculated for continuous data.

The ICC quantifies how much of the total variance in the measurements is due to true differences between subjects versus differences caused by raters or random error.

  • A high ICC (close to 1) means most of the variation reflects real differences between patients.
  • A low ICC means raters are inconsistent, so much of the variation is due to measurement error.
Example: Calculating inter-rater reliability with ICC
A longitudinal study examines how patients’ physical recovery progresses after knee replacement surgery. Over a six-month period, three physiotherapists independently rate each patient’s range of motion (in degrees) at monthly intervals.

Because the data is continuous (measured on a ratio scale) and there are multiple raters assessing the same subjects over time, the researchers use the ICC to measure inter-rater reliability.

There are several ICC models (depending on whether raters are fixed or random), but the most common is the two-way random effects model, which assumes all raters are randomly selected and rate all subjects. The formula for this model is:
ICC = \dfrac {{{MS_B-MS_W}}}{MS_B+(k-1)*MS_W}}
Where:

  • MSB = mean square between subjects (variation among subjects)
  • MSW = mean square within subjects (error + rater variance)
  • k = number of raters

These values come from a two-way ANOVA table.

Sample calculation

Suppose 10 patients are each rated by 3 physiotherapists on knee flexion (in degrees). After conducting the ANOVA, the researchers find:

  • MSB = 1200
  • MSW = 100
  • k = 3

ICC = \dfrac {{{1200-100}}}{1200+(3-1)*100}} = \dfrac {{{1100}}}{1400} = 0.79

The ICC of 0.79 indicates good agreement among the physiotherapists.

Percent agreement

The percent agreement method is the simplest way to assess inter-rater reliability. It measures the proportion of times that raters agree on a category or rating, without accounting for chance agreement like kappa does. This makes it less suitable for scientific research, but it is useful for preliminary checks or simple observational studies.

Example: Calculating inter-rater reliability with ICC
Researchers conduct a case study examining whether students correctly identify parts of a plant in a lab activity. Two observers independently record whether each of 30 students correctly labeled a given part as “root,” “stem,” or “leaf.”

A simplified table of agreements might look like this:

Rater 2: Correct Rater 2: Incorrect Total
Rater 1: Correct 15 3 18
Rater 2: Incorrect 2 10 12
Total 17 13 30

The formula to calculate percent agreement is:
Percent Agreement = \dfrac {{{Number of Agreements}}}{Total Observations}}*{100}
The number of agreements (where they both chose correct or where they both chose incorrect) is 15 + 10 (= 25).
Percent Agreement = \dfrac {{{25}}}{30}}*{100} = 83.3%
This means that in 83.3% of the cases, the observers gave the same rating.

Frequently asked questions about inter-rater reliability

What is the formula for calculating inter-rater reliability?

There isn’t just one formula for calculating inter-rater reliability. The right one depends on your data type (e.g., nominal data, ordinal data) and the number of raters.

  • Cohen’s kappa (κ) is commonly used for two raters
  • Fleiss’ kappa is typically used for three or more raters
  • The Intraclass Correlation Coefficient (ICC) is used for continuous data (interval or ratio). This is based on analysis of variance (ANOVA)

The most used formula (for Cohen’s kappa) is:
\kappa = \dfrac{{{P}_o}-{{P}_e}}{{1}-{P_e}}
Po is the observed proportion of agreement, and Pe stands for the expected agreement by chance.

What is inter-rater reliability in psychology?

In psychology, inter-rater reliability refers to the degree of agreement between different observers or raters who evaluate the same behavior, test, or phenomenon. 

It ensures that measurements are consistent, objective, and not dependent on a single person’s judgment, which is especially important in research, clinical assessments, and behavioral studies.

High inter-rater reliability indicates that results are dependable and reproducible across different raters.

What is a good inter-rater reliability score?

A good inter-rater reliability score depends on the statistic used and the context of the study.

For Cohen’s kappa (two raters), common guidelines are:

  • < 0.20: Poor agreement
  • 0.21–0.40: Fair agreement
  • 0.41–0.60: Moderate agreement
  • 0.61–0.80: Substantial agreement
  • 0.81–1.00: Almost perfect agreement

For the Intraclass Correlation Coefficient (interval or ratio data), similar thresholds are used:

  • < 0.50: Poor agreement
  • 0.51–0.75: Moderate agreement
  • 0.76–0.90: Good agreement
  • > 0.91: Excellent agreement

Cite this Quillbot article

We encourage the use of reliable sources in all types of writing. You can copy and paste the citation or click the "Cite this article" button to automatically add it to our free Citation Generator.

Merkus, J. (2025, October 24). What Is Inter-Rater Reliability? | Definition & Examples. Quillbot. Retrieved October 26, 2025, from https://quillbot.com/blog/research/inter-rater-reliability/

Cite this article
Is this article helpful?
0
Julia Merkus, MA

Julia has a bachelor in Dutch language and culture and two masters in Linguistics and Language and speech pathology. After a few years as an editor, researcher, and teacher, she now writes articles about her specialist topics: grammar, linguistics, methodology, and statistics.

Join the conversation

Please click the checkbox on the left to verify that you are a not a bot.

Do it all with QuillBot

Humanize AI
Paraphraser
Grammar Checker
AI Detector
Plagiarism Checker
Translate
Summarizer
Sentence Rewriter
Rewording Tool
Word Counter
Paragraph Rewriter
AI Proofreader
Spell Checker
Punctuation Checker
Essay Checker
Citation Generator
APA Citation Generator
MLA Citation Generator
Chicago Citation Generator
AI Chat
Ask AI
AI Search
AI Paragraph Generator
AI Story Generator
AI Email Writer
AI Text Generator
AI Writer
Cover Letter Generator
AI Acronym Generator
AI Title Generator
Hashtag Generator
AI Lyric Generator
AI Product Name Generator
AI Meta Description Generator
AI Instagram Caption Generator
AI Product Title Generator
AI Caption Generator
AI Job Description Generator
AI Article Rewriter
AI Image Generator
Background Remover
Image to Text
AI Logo Generator
AI Tatto Generator
AI Art Generator
AI Character Generator
AI Background Generator
AI Random Image Generator
Chat PDF
PDF Editor
PDF Converter
PPT to PDF
Word to PDF
JPG to PDF
PDF to JPG
PDF to PPT
PNG to PDF
Excel to PDF
Speech To Text
QR Code Generator
Invisible Character
Text to Speech
View all

Others also liked

What Is a Conceptual Framework? | Examples & Tips

A conceptual framework illustrates the connections between different variables in a study.
19

Purposive Sampling | Definition & Examples

Purposive sampling is a sampling method where individuals are intentionally selected because they have specific qualities.

What Is Convergent Validity? | Definition & Examples

Convergent validity captures how similar a test is to other tests that measure the same construct.